この記事では一般常識で解ける簡単な問題から、算数オリンピックや難関中学の入試を参考に作ったもの。そして私のオリジナルも含め全部で15問挙げています。
ガチで解きたい方は解答を見ないように慎重にスクロールしてください。
算数・数学15連発
50個作るのにかかる時間
ある工場では機械が10台あり、ボールを10個作るのに10分かかります。
では機械が50台ある場合、ボールを50個作るのに何分かかるでしょう。
解答
機械が1台だけであれば、ボールを50個作るまでに10×5=50分かかります。
しかし、機械は50台あるのですから、1台で1個に振り分ければ10分で済みます。
よって、答えは10分です。
トーナメントの試合数
100チームでトーナメント戦を行ったとき、試合数はいくつになるでしょう。
ただし、引き分けはないものとします。
解答
100チームでトーナメントを行なったとき、優勝するのは当然1チームだけです。
ということは、100チーム中99チームがトーナメントで負けているわけです。
だからこれは負けたチーム数=試合数と言えます。
よって、答えは99試合。
1000日後の曜日
今日を月曜日としたとき、1000日後は何曜日ですか。
解答
これは割り算ができれば小学生でも簡単に解けます。
1週間は7日ですから、1000を7で割り、その余りを求めれば答えを導きだせます。
1000割る7は142余り6。つまり、1000日後は6日後(1日前)と同じ曜日ということです。
したがって、月曜日の6日後、日曜日が答えとなります。
長針と短針が重なる時間
1時から2時の間で、長針と短針が重なるのは何時何分でしょう。
小数第1位を四捨五入して整数で答えてください。
解答
まず最初に長針と短針が1分間に動く角度を求めます。
短針は1時間で30度動きますから1分間で0.5度、長針は1時間で360度動くので1分間で6度動きます。
1時の時点で長針は12、短針は1の地点にあるので、長針は1分間に5.5度短針に近づいていることになります。
よって、答えは30÷5.5≒5.45(正確には60/11)より1時5分です。
ピッタリ重なる瞬間を見たい方は1時5分27秒まで待ちましょう。
数字をよく見れば分かる
8628=3
6684=3
5490=2
1743=1
7347=?
?に当てはまる数字は何でしょう。
解答
算数の問題として挙げていますが、計算力はまったく必要ありません。
右辺にある数字は、4桁の数字のうち、180度回転させると別の数字(9と6)になるか、数字が変わらないもの(0、1、8)がいくつあるかを示しています。
7347はどちらも当てはまりませんので、答えは0です。
追記
コメントで『「直線を使わない数字」の数』という別解をいただきました。この定義に従うと、
8628=3
6684=3
5490=2
1743=1
7347=1
になります。
2種類のお金しかない世界
ある国では3円玉と4円玉の2種類しかお金がありません。
10円以上のすべての金額を、おつりを貰わずに支払うことはできますか。
できないときはその金額を答えてください。
解答
2種類だけだとおつりなしでは払えないように思えますが、実際に確かめてみましょう。
10円 3円玉2枚+4円玉1枚
11円 3円玉1枚+4円玉2枚
12円 3円玉4枚or4円玉3枚
13円 3円玉3枚+4円玉1枚
14円 3円玉2枚+4円玉2枚
15円 3円玉5枚or3円玉1枚+4円玉3枚
16円 4円玉4枚or3円玉4枚+4円玉1枚
17円 3円玉3枚+4円玉2枚
18円 3円玉6枚or3円玉2枚+4円玉3枚
19円 3円玉5枚+4円玉1枚or3円玉1枚+4円玉4枚
20円以上の金額は上記の金額に10円ずつ足せば払えることが分かります。
なので、問題の答えは「おつりなしで支払うことはできる」です。
3人で仕事をすると何日かかる?
ある仕事をこなすのにAは5日、Bは6日、Cは7日半かかります。
3人で行うと何日かかるでしょう。
解答
仕事算の3人バージョンです。
仕事全体の量を30とすると、すべてこなすのにAは30÷5=6、Bは30÷6=5、Cは30÷7.5=4かかります。
合計は6+5+4=15なので、3人で30の仕事をこなすには30÷15=2かかります。
よって、答えは2日です。
バッドとボールの値段
A君は野球用品でバット1本とボール1個を買いました。
値段は2つ合わせて11000円で、バットの値段はボールよりも10000円高いです。
さて、ボールの値段はいくらでしょう。
解答
これは比較的有名なひっかけ問題です。
直感だと1000円と答えそうですが、それだとバットは10000円となり、金額差は9000円で計算が合いません。
ボールの値段をx、バットの値段をyとすると、以下の連立方程式が成り立ちます
x+y=11000
y=x+10000
x+y=11000のyに、x+10000を代入して式を整理すると
2x=1000
x=500
よって、ボールの値段は500円です。
テストの平均点
AとBは5教科のテストを受けました。テストはすべて100点満点です。
どちらかは全教科で90点以上を取っていて、2人の合計の差は31点です。
また、全教科の合計にAは1点、Bは2点加えると平均点は2人とも整数になります。
Aの合計点数が7で割りきれるとき、2人の平均点をそれぞれ求めてください。
解答
全教科で90点以上取っているので、AとBのどちらかは合計が450点以上です。
また、Aは全教科の合計に1点、Bは2点加えると平均点は2人とも整数になります。
平均点が整数になるのは合計の1の位が0または5のときなので、Aの合計は1の位が4か9、Bの合計は1の位が3か8だと分かります。
仮にA<BとしてBが453点だとすると、Aは422点。458点としてもAは427点となり計算が合いません。ということで、全教科で90点以上取ったのはAです。
Aの合計は454、459、464、469、474、479の6通り考えられます(484点以上だとBも450点以上取ったことになる)が、7で割りきれるのは469だけ。
したがって、Aの平均点は469÷5=93.8点、Bの平均点は438÷5=87.6点
通分するのは非常に面倒
次の式の計算結果を求めてください。
解答
難関中学ではこのような計算問題がよく出題されます。ただ、実際の入試ではより複雑になることが多いです。
普通に計算するのはあまりにも非効率なので、以下のような工夫を施します。
1/6=1/2-1/3
2/15=1/3-1/5
2/35=1/5-1/7
2/63=1/7-1/9
1/90=1/9-1/10
式を見れば分かるように、-1/3+1/3、-1/5+1/5、-1/7+1/7、-1/9+1/9の和はすべて0になります。
残ったのは1/2と-1/10だけです。
したがって、答えは1/2-1/10=2/5
辺の長さは何㎝か
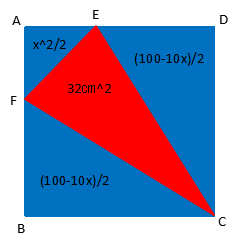
下の図において、四角形ABCDは一辺が10㎝の正方形、三角形CEFは面積が32平方センチメートルの二等辺三角形です。
解答
まずは三角形BCFと三角形DCEについて考えます。
問題文から、BC=DC、CF=CE、∠CBF=∠CDE=90度であることが分かるので、三角形BCFと三角形DCEは直角三角形です。
この2つの三角形は、斜辺と他の1辺がそれぞれ等しいので合同です。

これは直角三角形の合同条件で、もう1つは「斜辺と1つの鋭角がそれぞれ等しい」です。
それではAEの長さを求めていきます。
線AEの長さをxと置くと、線DEは10-xと表せます。
三角形DCEの面積を式で表すと10(10-x)/2=(100-10x)/2、三角形BCFと三角形DCEは合同なので2つの面積の和は100-10x、三角形AEFの面積はx^2/2です。
3つの三角形の和は式で表すとx^2/2+100-10x=68で、両辺を2倍して式を整理するとx^2-20x+64=0となります。
この方程式を解くと、因数分解して(x-4)(x-16)=0から、x=4,x=16
線AEは10㎝未満なので、答えは4㎝です。
主張は正しい?
以下はとあるカップルの会話です。
「明日晴れたら君の家に遊びに行くよ」
「分かった。楽しみにしてるね」
しかし、翌日は生憎の雨でした。
「なんで家に来てくれなかったの」
「雨だからだよ。間違ったことは言ってない」
さて、彼の主張は正しいと言えるでしょうか。
解答
最初に彼氏は「明日晴れたら君の家に遊びに行くよ」と言いました。
晴れなかった場合には何も言っていないので、天気が晴れでも雨でも矛盾は生じません。
よって、彼の主張は正しいと言えます。ただ、リアルだと彼のようなタイプは好まれないでしょうね。
名字のパラドックス
日本の名字は全部で30万種類あると言われています。
1つの場所に人をランダムに集めたとき、同じ名字のペア(親子や兄妹は除く)ができる確率が50%を超えるのは、次のうちどれ?
ア.646人
イ.851人
ウ.984人
エ.1176人
オ.1663人
解答
これは『誕生日のパラドックス』と呼ばれる、「何人集めれば、同じ誕生日のペアができる確率が50%を超えるか」というものを名字に置き換えた問題です。
で、肝心の正解ですがアの646人です。意外と少ない。
ちなみに、イの851人を集めると70%、ウの984人は80%、エの1176人は90%、オの1663人は99%を超える確率で、同じ名字のペアが1組できます。
激レアキャラが当たる確率
アプリゲームのガチャで、0.1%の確率で当たる激レアキャラクターがいるとします。
1000回ガチャを引いたとき、激レアが当たる確率は何%でしょう。以下の5つから選んでください。
ア.56%
イ.64%
ウ.78%
エ.82%
オ.100%
解答
直感だと「1000回引いたんだから100%じゃないの?」と思いがちですが、正解はイの64%(小数点以下四捨五入)です。
倍の2000回引いても約86%、2302回引いてやっと当たる確率が90%を超えます。
当たる確率が99%を超えるのに必要な回数は4603回。1回200円としても92万円600円消費します。
2枚のカードの数字は何?
CはAとBに、数字の書かれたカードを1枚ずつ渡しました。AとBは相手の持っているカードの数字を知りません。
C「2枚とも1以上の自然数が書かれています。数字の差は200です」
その後、CはAにたずねました。
C「Aさん、B君の持っているカードの数字が分かりますか」
A「分かりません」
C「B君はどうですか」
B「僕も分かりません」
A「B君の持っているカードの数字が分かりました。2枚とも数字が1大きかったら、まだ分かりませんでした」
2人の持っているカードの数字は何でしょう。
解答
1994年に算数オリンピックで出題された問題を改題したものです。
Aは最初、CにBのカードの数字が何かたずねられて「分かりません」と答えました。
仮にAの数字が200だとすると、Cがたずねた時点で、AはBのカードの数字が400だと容易に推測できます。なので、Aのカードは201以上の数字が書かれています。
一方のBも、Cにたずねられて「僕も分かりません」と答えました。Aのカードが201以上なのはすでに分かっているので、Bの持っているカードは401以上の数字だと分かります。
数字を大きくして、Aのカードが600として考えてみます。200と仮定したときと同様に、Cがたずねた時点では、AはBのカードが400か800か判断できません。
しかし、BのセリフからAはBの持っているカードの数字が401以上、つまり800だと断定できます。
それより1大きい場合、Aのカードが601、Bのカードが801だと、AはCとBのセリフを聞いてもBのカードの数字を当てることはできません。
よって、カードの数字はAが600、Bは800です。
まとめ
説明が少々雑なところもありますが、どうかご容赦ください。
最後の問題は初見だと大人でも苦戦すると思います。
実際に出題された問題は正答率がわずか1%。小学生が解くには難しすぎたのかもしれません。
名字と激レアキャラの問題は計算量が膨大なので筆算で解くのは正直無理です。私はExcelの力を借りました。

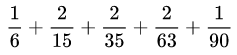
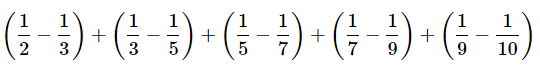


これ、べんきょうになりました。ありがとうございます!
こちらこそ、コメントありがとうございます。
楽しく読ませていただきました。
『数字をよく見れば分かる』は、
「直線を使わない数字」の数
7347=1
という別解はいかがでしょうか。
コメントありがとうございます。面白い解答ですね。追記しておきますので少々お待ちください。。